Appendix A — Pseudo-log transformations

A.1 Introduction

This supplemental section illustrates how pseudo-log transformations can be used to transform skewed distributions towards normality.

The transformation \(f(x) = sinh^-1(x/2\sigma)/log(10)\) is a pseudo-logarithmic transformation mentioned by (Johnson 1949). It has the following advantages over ordinary logarithmic transformations:

  • it is defined also for \(x=\) as \(f(0) = 0\)
  • it is a signed logarithmic transformation, and is defined also for negative values as \(f(-|x|)=-f(|x|)\)

Of course, this comes at the cost of deviation from the logarithmic transformation in terms of interpretability.

The parameter \(\sigma\) may be used to adapt the transformation to a specific range of an empirical distribution.

We define the pseudo-logarithmic transformation in R as:

Code 
pseudo_log <-
  function(x, sigma = 1, base = 10)
    asinh(x / (2 * sigma)) / log(base)

inv_pseudo_log <-
  function(x, sigma = 1, base = 10)
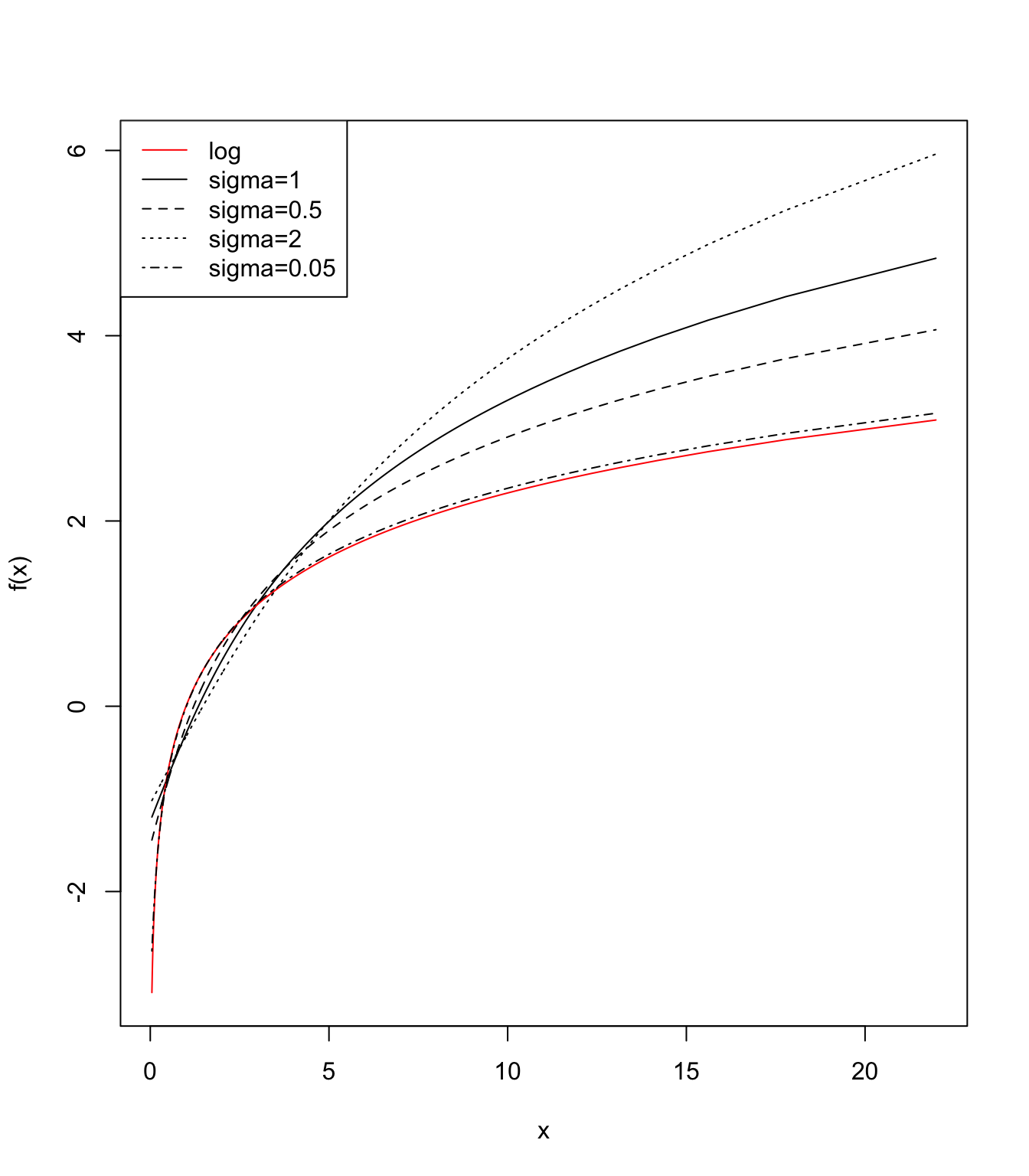
    2 * sigma * sinh(x * log(base))

A.2 Impact of choice of \(\sigma\)

Next, we investigate how the parameter \(\sigma\) impacts the result of the transformation. We assume that \(x\) follows a log-normal distribution, and we will show results of \(f(x)\) with different choices of \(\sigma\). We center and scale \(f(x)\) before plotting.

Code 
p <- seq(0.001, 0.999, 0.001)
x <- exp(qnorm(p, mean = 0, sd = 1))

hist(x)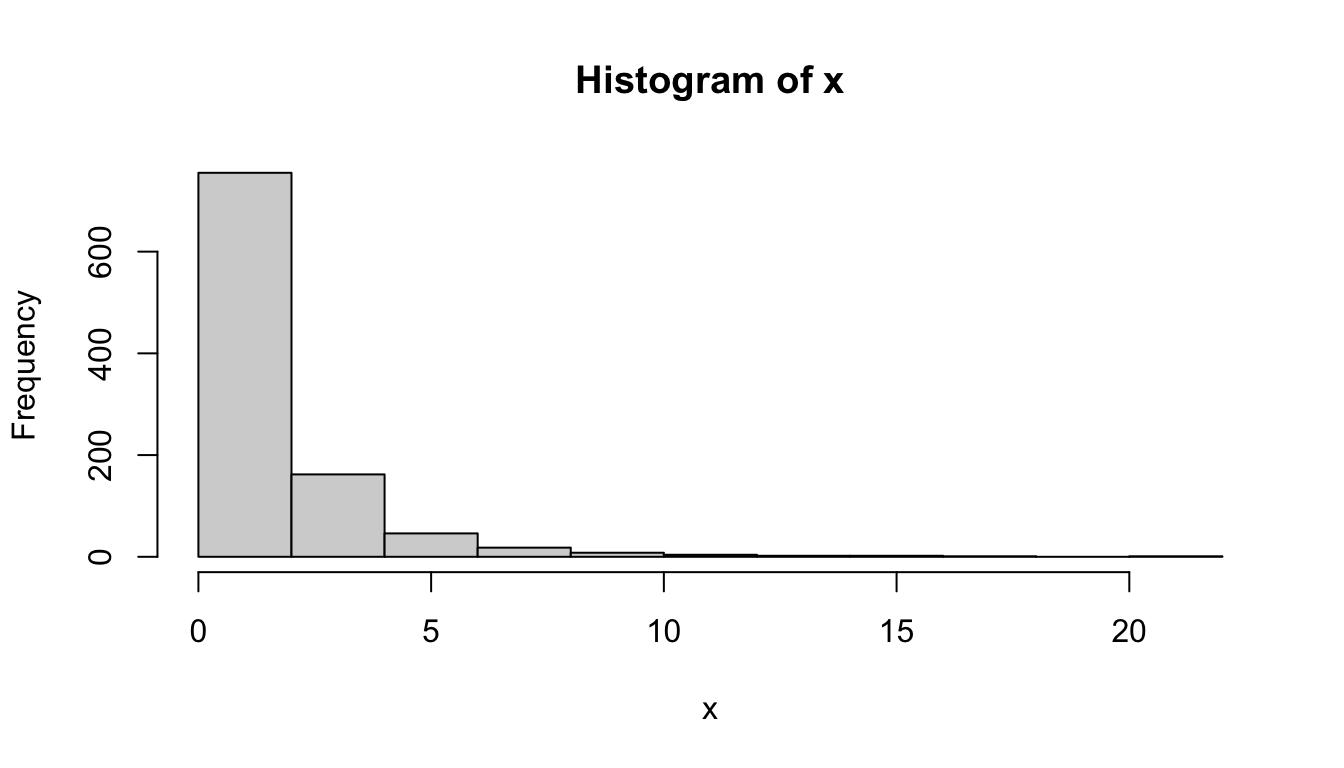

Code 
y <-
  cbind(
    log(x),
    scale(pseudo_log(x, 1)),
    scale(pseudo_log(x, 0.5)),
    scale(pseudo_log(x, 2)),
    scale(pseudo_log(x, 0.05))
  )

plot(x,
     y[, 2],
     type = "l",
     ylab = "f(x)",
     ylim = range(y))
lines(x, y[, 1], col = "red")
lines(x, y[, 3], type = "l", lty = 2)
lines(x, y[, 4], type = "l", lty = 3)
lines(x, y[, 5], type = "l", lty = 4)
legend(
  "topleft",
  lty = c(1, 1, 2, 3, 4),
  col = c("red", "black", "black", "black", "black"),
  legend = c("log", "sigma=1", "sigma=0.5", "sigma=2", "sigma=0.05")
)

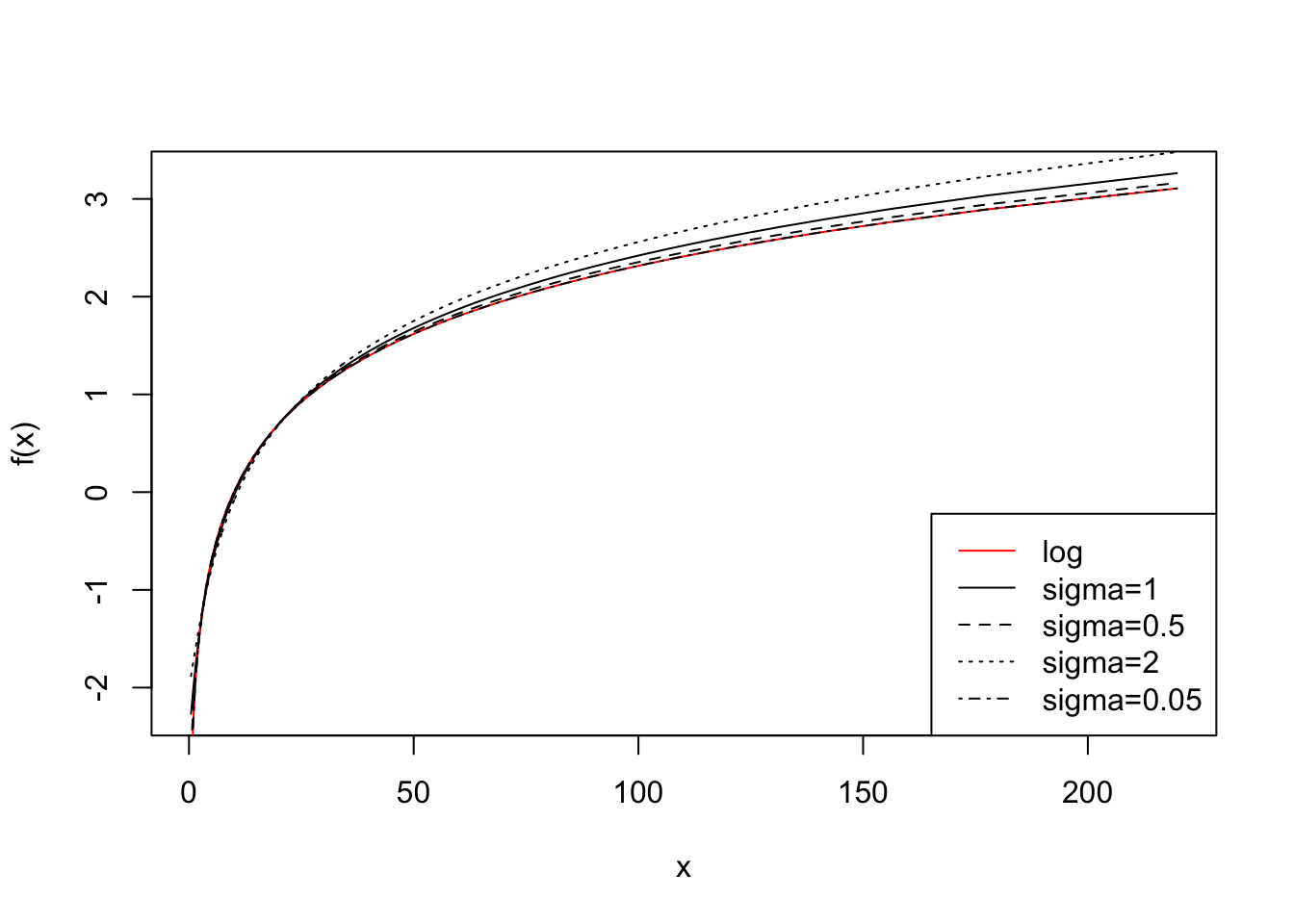
In the next code chunk, we multiply by 10 and repeat the exercise. We learn that the transformations become more similar and the choice of \(\sigma\) less relevant.

Code 
x <- x * 10

y <-
  cbind(
    scale(log(x)),
    scale(pseudo_log(x, 1)),
    scale(pseudo_log(x, 0.5)),
    scale(pseudo_log(x, 2)),
    scale(pseudo_log(x, 0.05))
  )


plot(x, y[, 2], type = "l", ylab = "f(x)")
lines(x, y[, 1], col = "red")
lines(x, y[, 3], type = "l", lty = 2)
lines(x, y[, 4], type = "l", lty = 3)
lines(x, y[, 5], type = "l", lty = 4)
legend(
  "bottomright",
  lty = c(1, 1, 2, 3, 4),
  col = c("red", "black", "black", "black", "black"),
  legend = c("log", "sigma=1", "sigma=0.5", "sigma=2", "sigma=0.05")
)

Finally, we apply the pseudo-logarithmic transformation to the original normal deviates. We learn that a higher value for the parameter \(\sigma\) makes the distribution ‘slimmer’ while a lower value makes it ‘fatter’, and it is even possible to induce bimodality with low values of sigma:

Code 
z <- qnorm(p, mean = 0, sd = 1)
hist(z)
hist(pseudo_log(z, sigma = 1))
hist(pseudo_log(z, sigma = 2))
hist(pseudo_log(z, sigma = 0.5))
hist(pseudo_log(z, sigma = 0.05))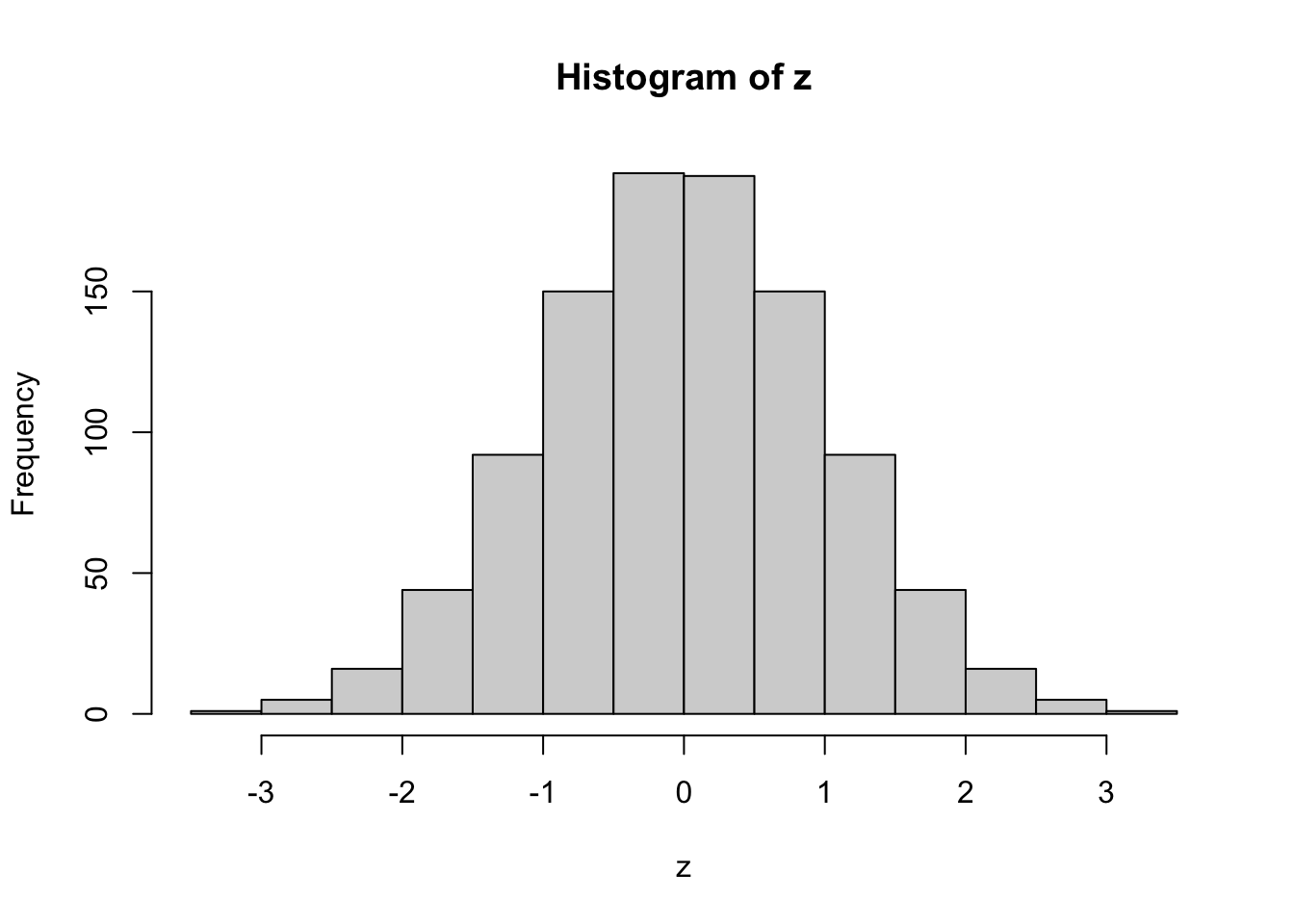

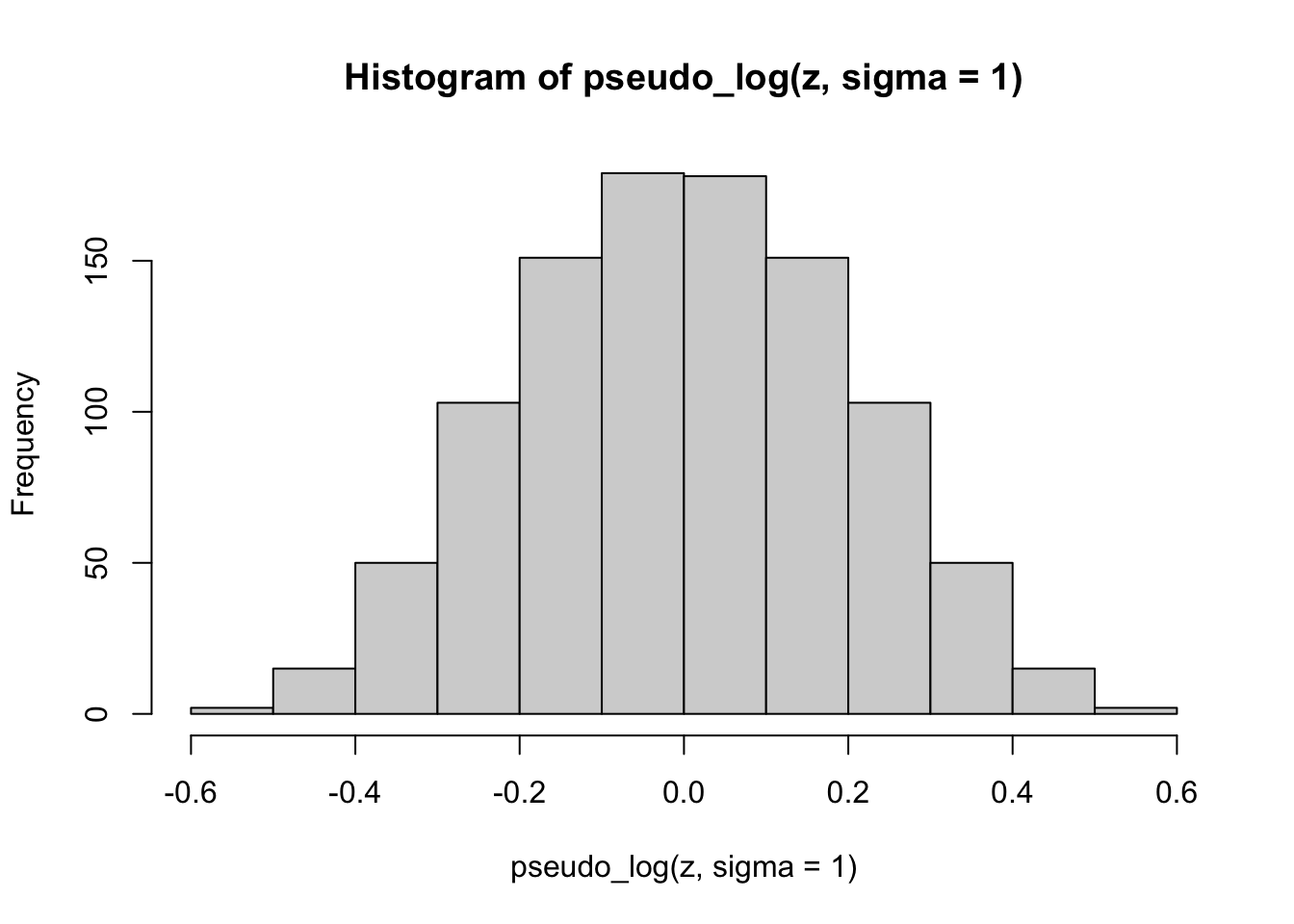
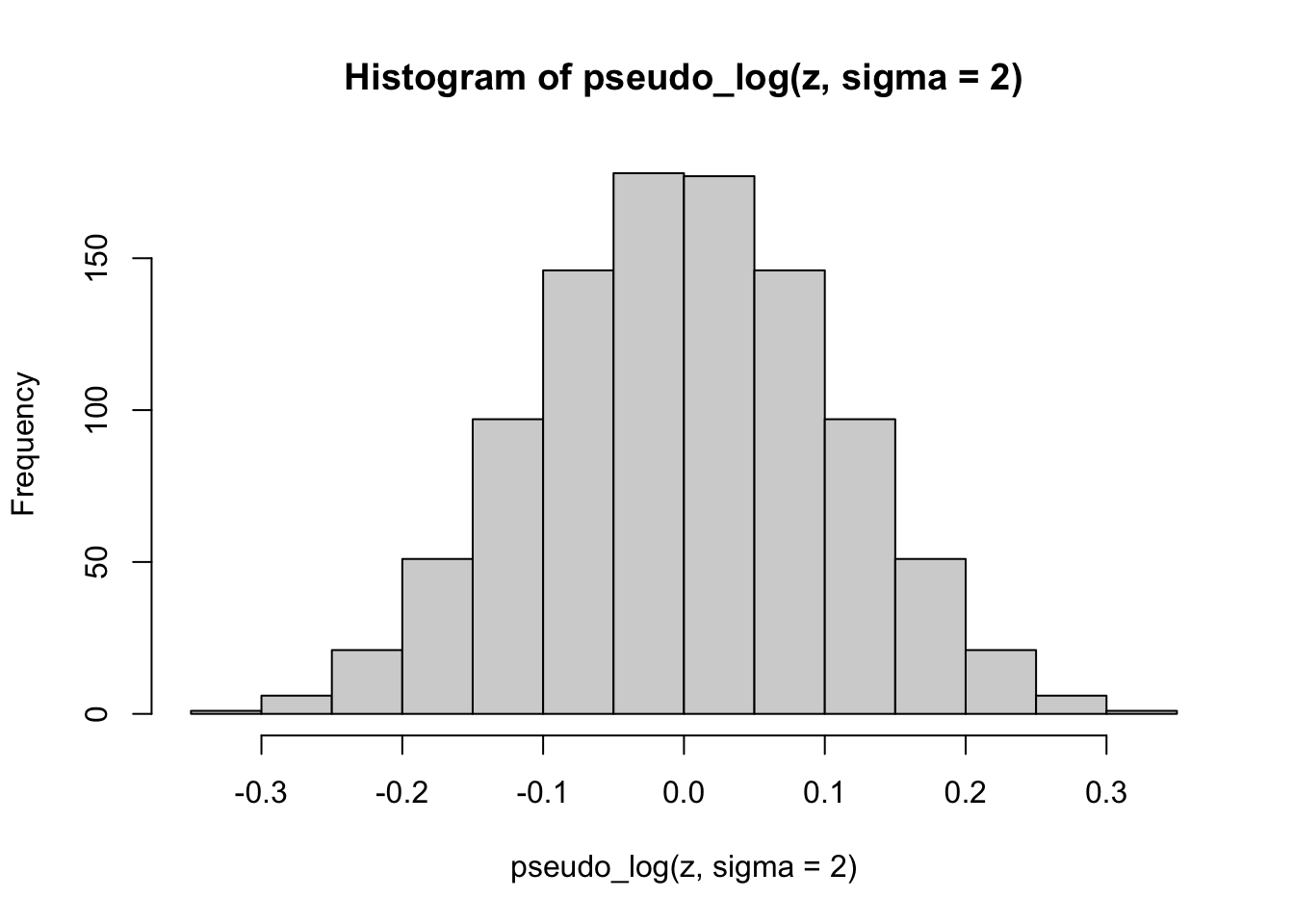
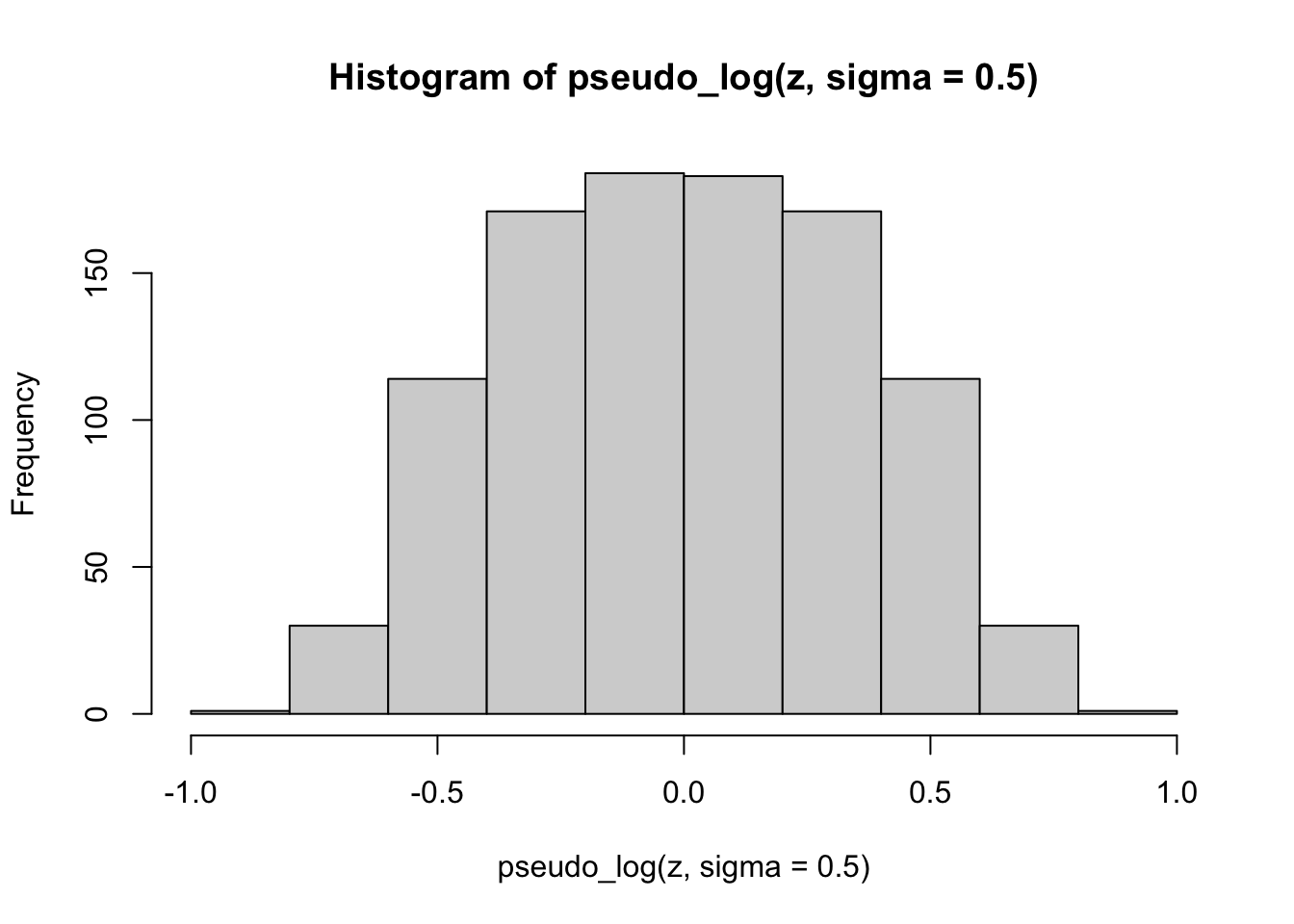
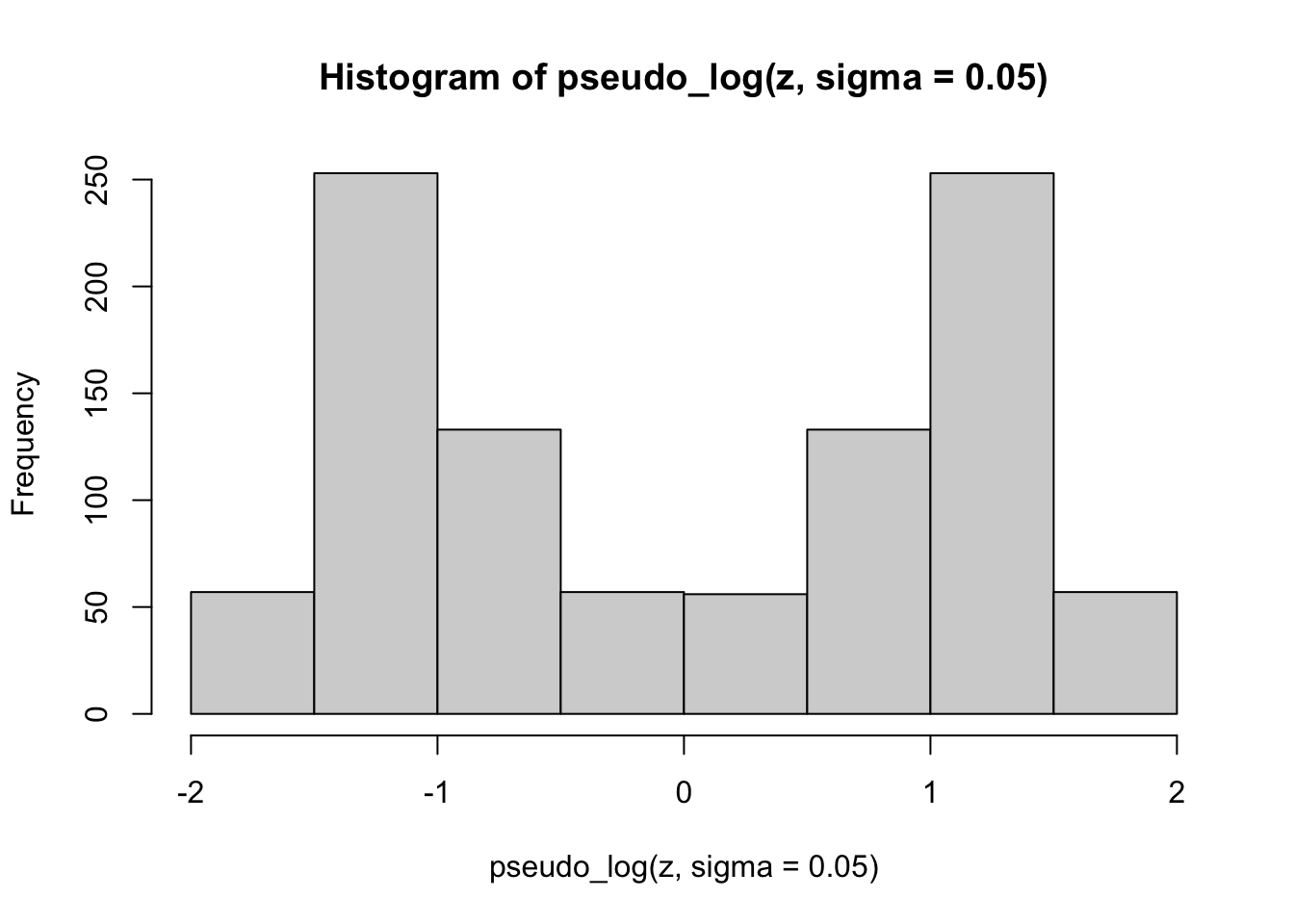
A.3 Finding a parameter that best achieves normality

Any test statistic for testing normality could be chosen to find a suitable value of \(\sigma\) that induces normality into the transformed values. Here we use the (Pearson) correlation coefficient to compare the empirical distribution with normal deviates.

A.3.1 Deviates from log normal distribution

We simulate from a shifted log normal distribution and evaluate the value of \(\sigma\) that optimizes agreement with a normal distribution:

Code 
# #| layout-ncol: 2    #Remark. did not render nicely in docx (GH)

x <- sort(exp(rnorm(1000) + 3))

hist(x)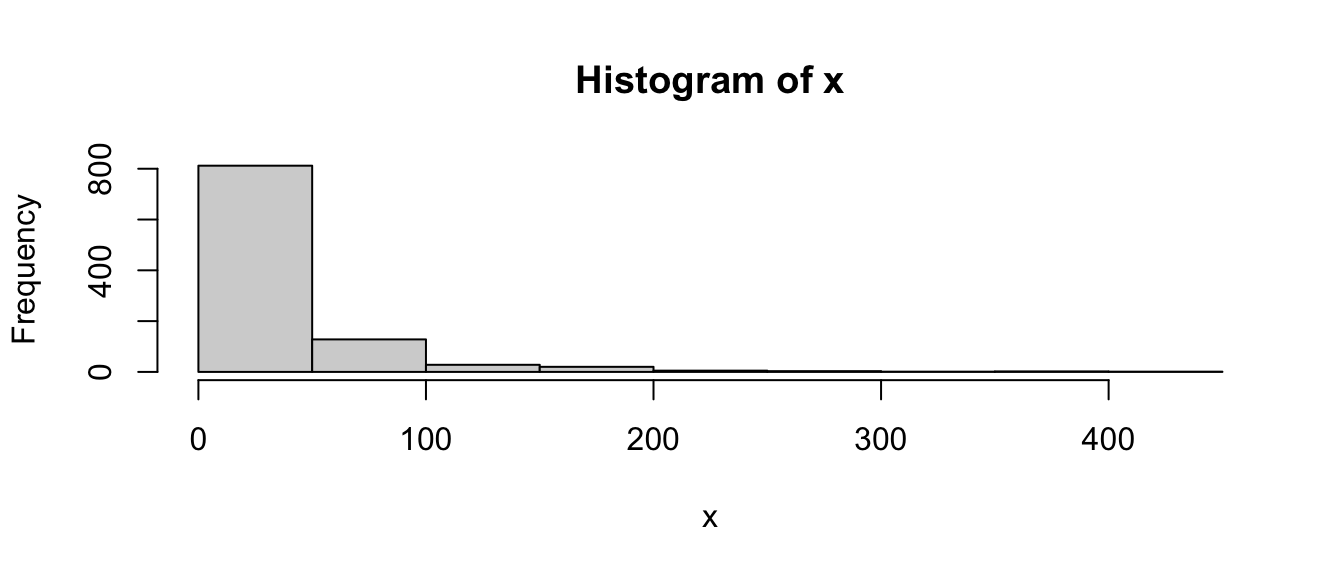

Code 
sigmas <- 2 ** seq(-10, 10, 1)
origcor <- cor(qnorm((1:length(x) - 0.5) / length(x)), x)

ncorx <-
  sapply(sigmas, function(X)
    cor(qnorm((1:length(
      x
    ) - 0.5) / length(x)), pseudo_log(x, X)))

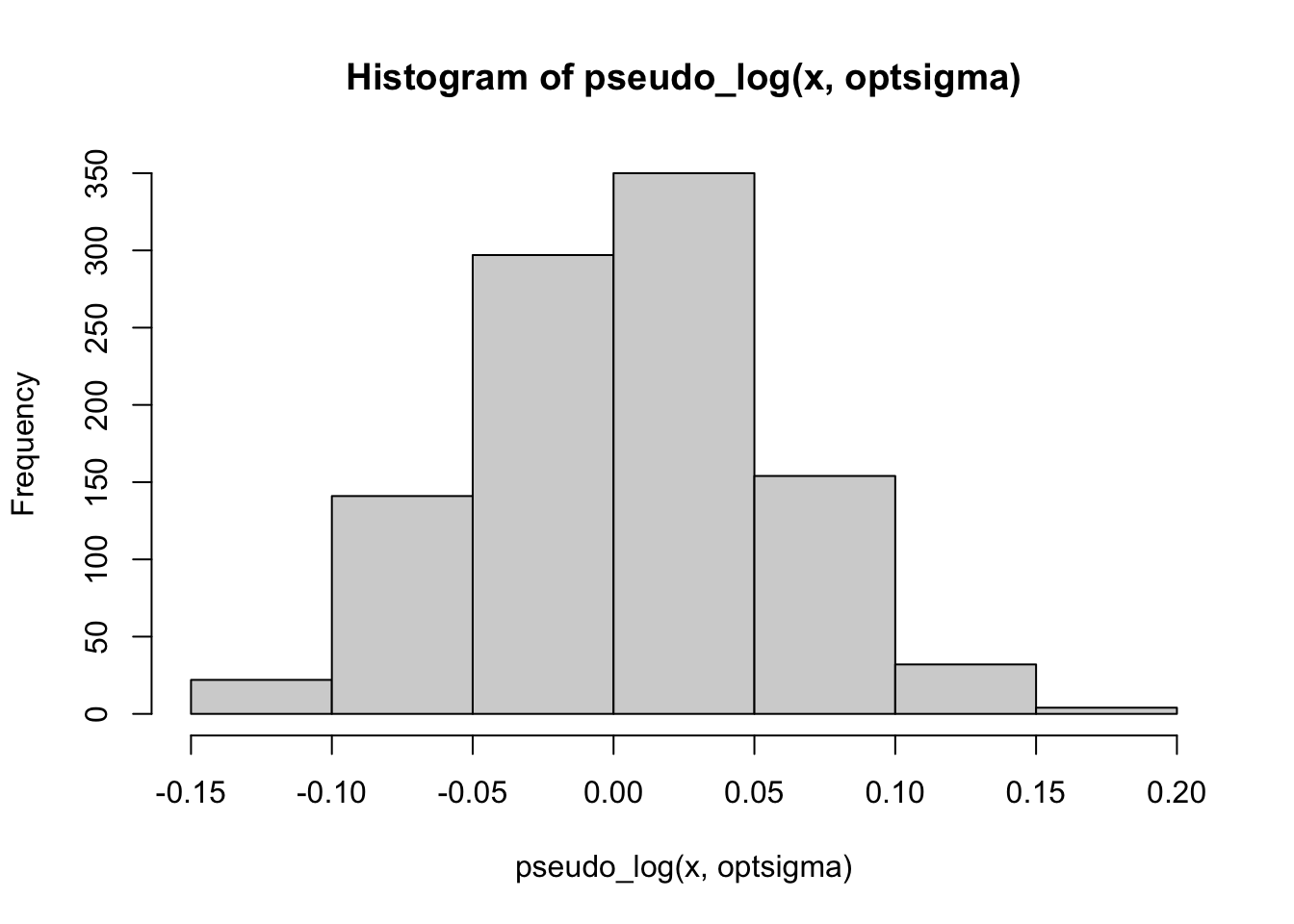
cat("Optimal sigma: ")
Optimal sigma:
Code 
(optsigma <- sigmas[ncorx == max(ncorx)])
[1] 0.25
Code 
plot(log2(sigmas), ncorx, ylab = "Correlation with normal deviates", ylim =
       c(0, 1))
points(log2(sigmas)[ncorx == max(ncorx)], max(ncorx), pch = 19)
abline(h = origcor)
legend(
  "bottomright",
  lty = c(1, NA, NA),
  pch = c(NA, 1, 19),
  legend = c("Original", "Pseudo-log", "Pseudo-log with optimal sigma")
)
box()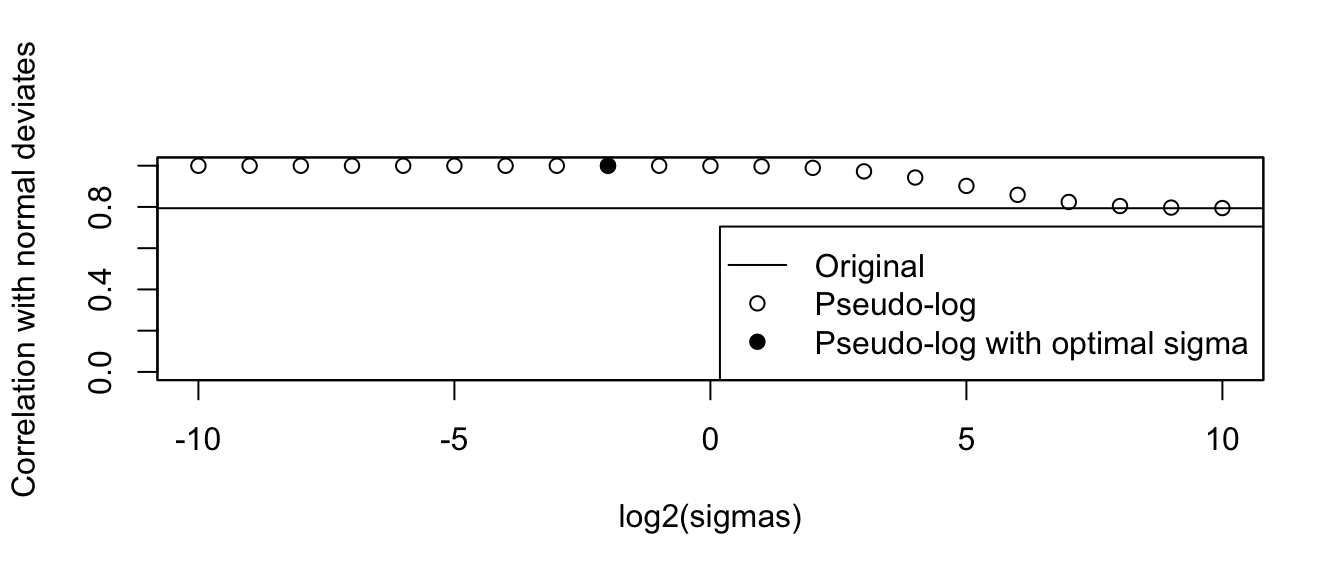

Code 
hist(pseudo_log(x, optsigma))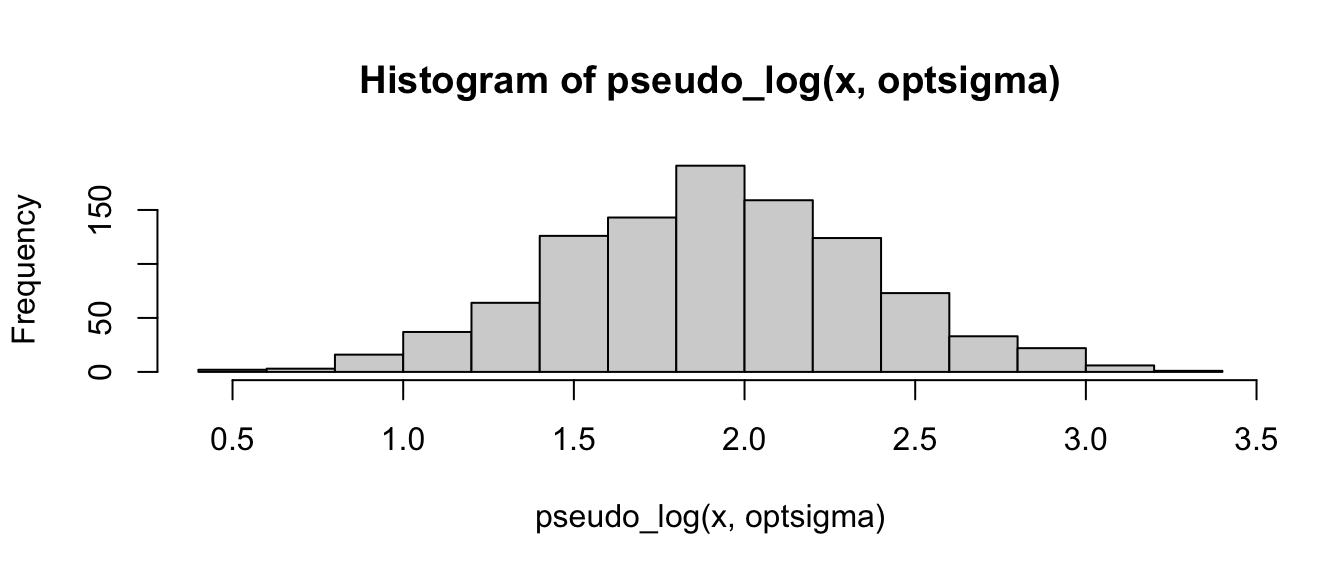

A.3.2 Deviates from exponential distribution

Also with an exponential distribution, the pseudo-logarithm may achieve a better agreement with a normal:

Code 
x <- sort(exp(rnorm(1000) + 3))

hist(x)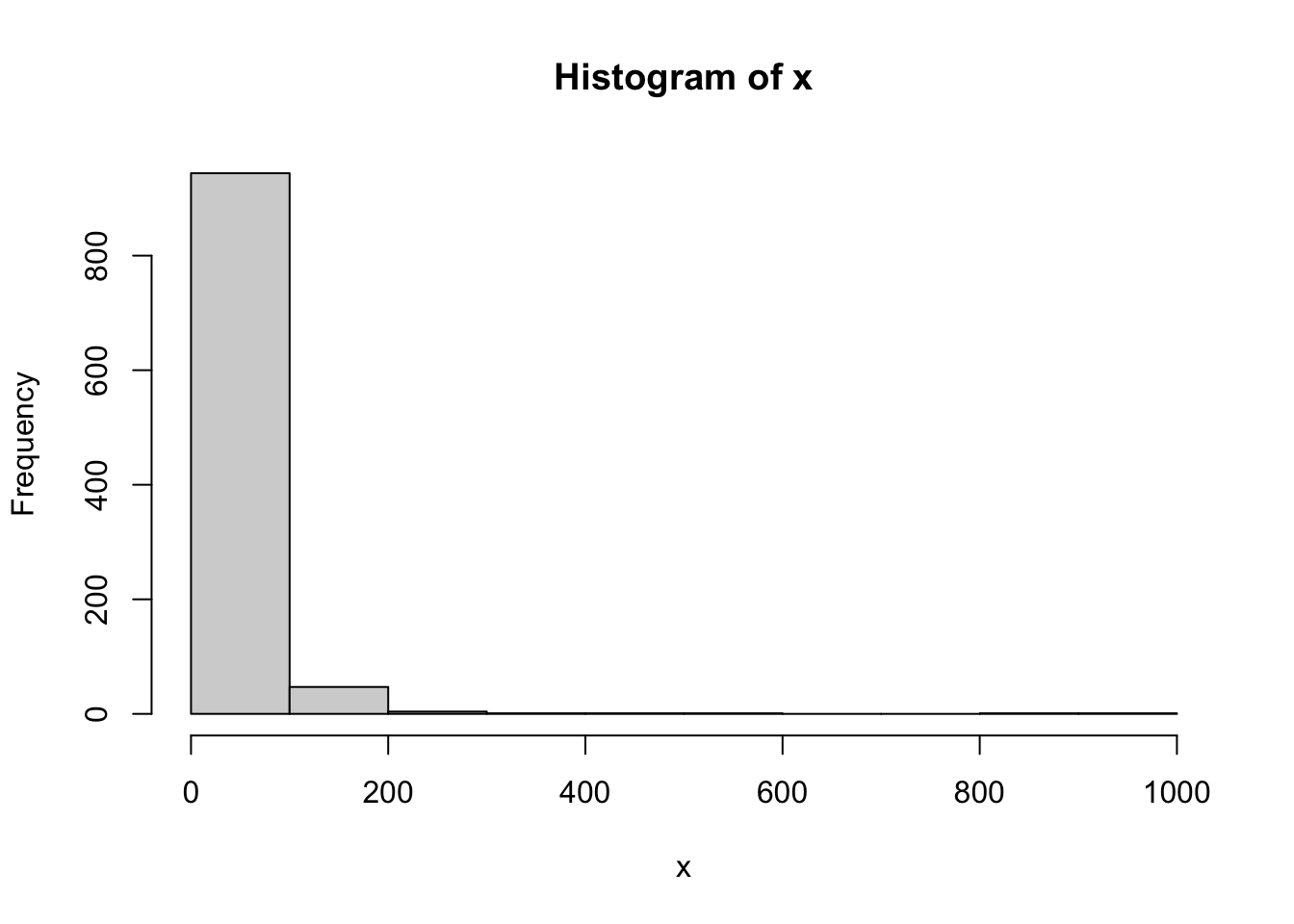

Code 
sigmas <- 2 ** seq(-10, 10, 1)
origcor <- cor(qnorm((1:length(x) - 0.5) / length(x)), x)

ncorx <-
  sapply(sigmas, function(X)
    cor(qnorm((1:length(
      x
    ) - 0.5) / length(x)), pseudo_log(x, X)))

cat("Optimal sigma: ")
Optimal sigma:
Code 
(optsigma <- sigmas[ncorx == max(ncorx)])
[1] 0.0009765625
Code 
plot(log2(sigmas), ncorx, ylab = "Correlation with normal deviates", ylim =
       c(0, 1))
points(log2(sigmas)[ncorx == max(ncorx)], max(ncorx), pch = 19)
abline(h = origcor)
legend(
  "bottomright",
  lty = c(1, NA, NA),
  pch = c(NA, 1, 19),
  legend = c("Original", "Pseudo-log", "Pseudo-log with optimal sigma")
)
box()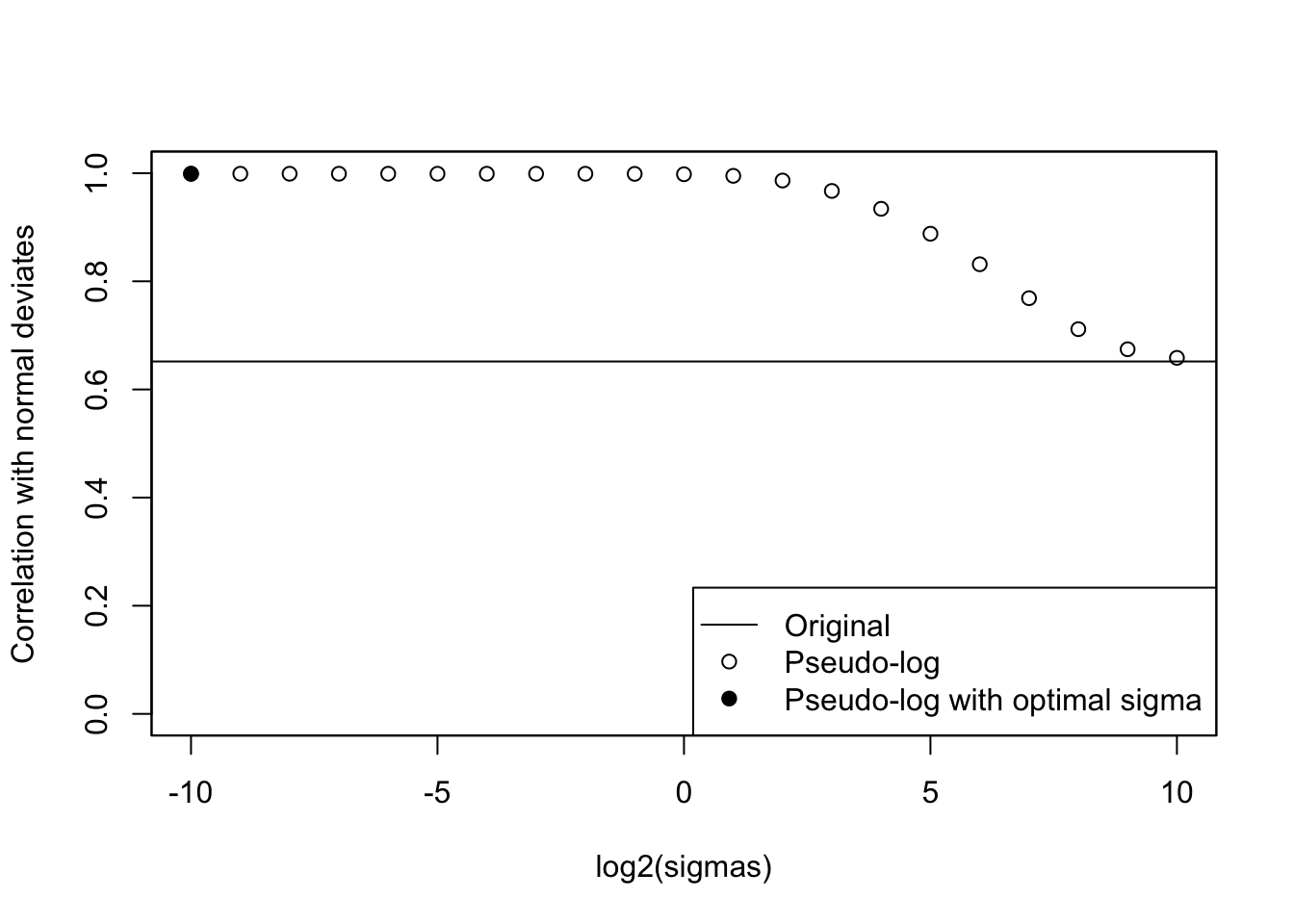

Code 
hist(pseudo_log(x, optsigma))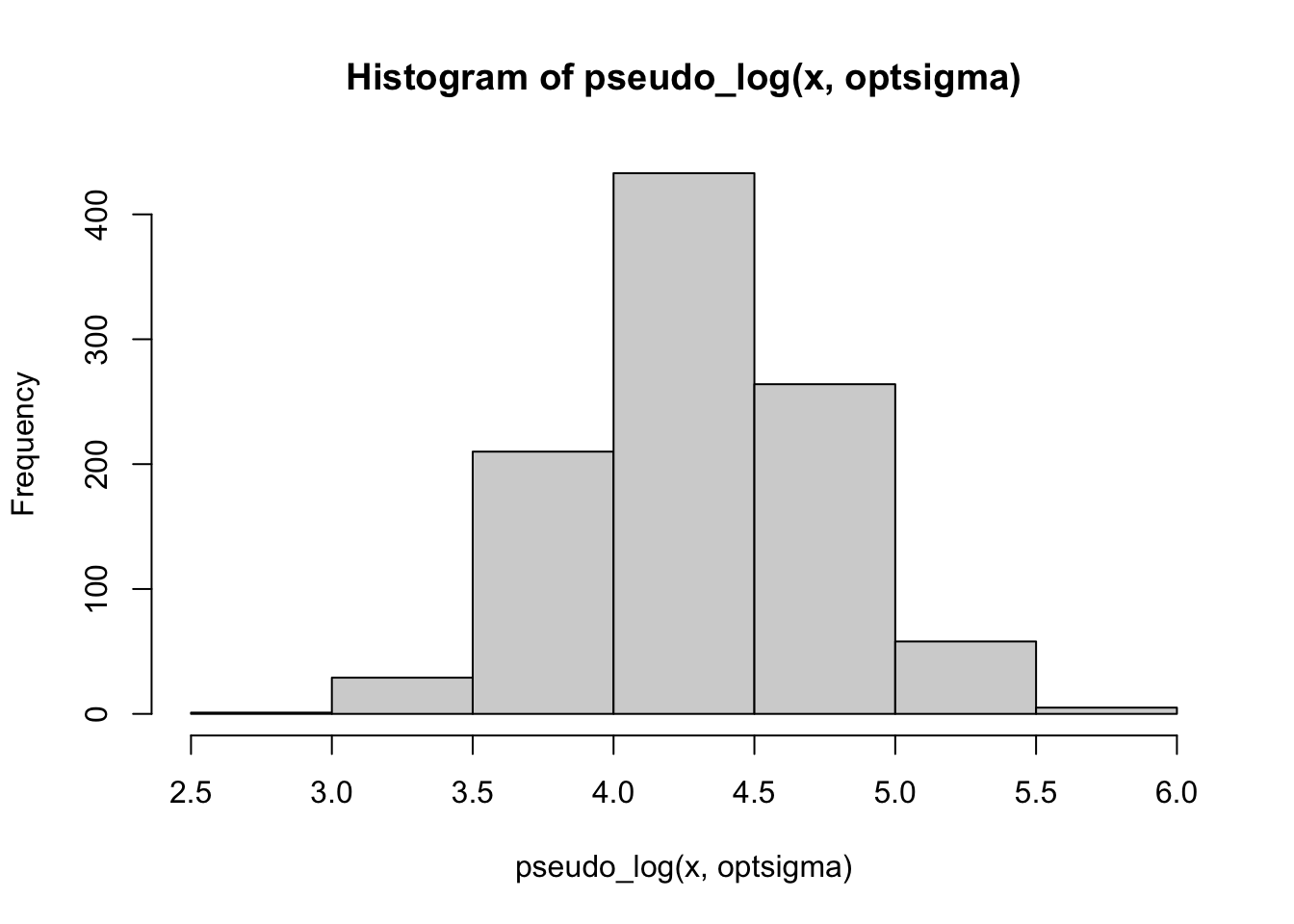

A.3.3 Deviates from mixture distribution

Now we mix a normal, lognormal and exponential distribution:

Code 
x1 <- scale(rnorm(1000))
x2 <- scale(rexp(1000))
x3 <- scale(exp(rnorm(1000)))

p1 <- rbinom(1000, 1, 0.33)
p2 <- rbinom(1000, 1, 0.5)

x <- p1 * x1 + (1 - p1) * (p2 * x2 + (1 - p2) * x3)
x <- x - min(x)
x <- sort(x)

hist(x)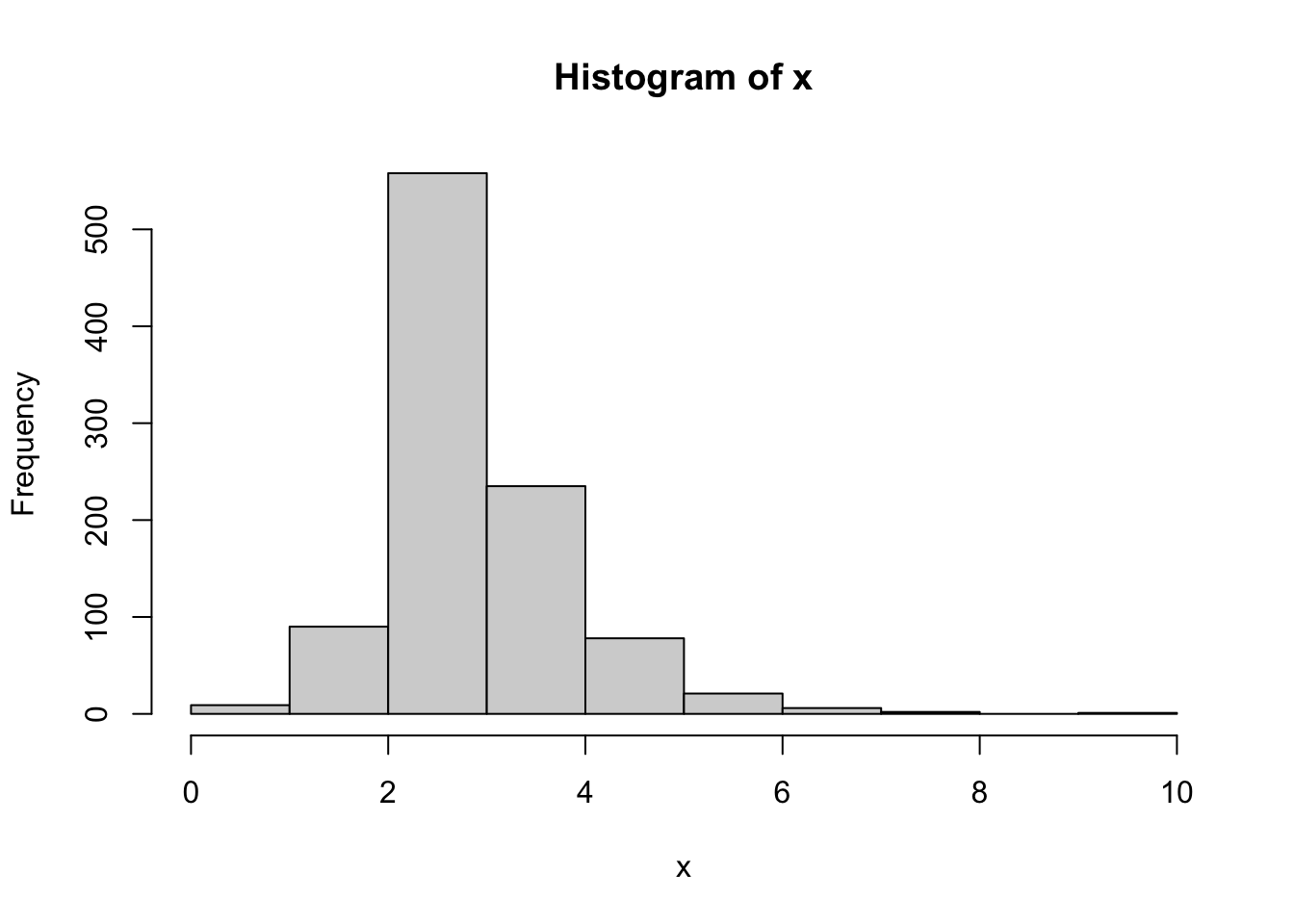

Code 
sigmas <- 2 ** seq(-10, 10, 1)
origcor <- cor(qnorm((1:length(x) - 0.5) / length(x)), x)

ncorx <-
  sapply(sigmas, function(X)
    cor(qnorm((1:length(
      x
    ) - 0.5) / length(x)), pseudo_log(x, X)))

cat("Optimal sigma: ")
Optimal sigma:
Code 
(optsigma <- sigmas[ncorx == max(ncorx)])
[1] 1
Code 
plot(log2(sigmas), ncorx, ylab = "Correlation with normal deviates", ylim =
       c(0, 1))
points(log2(sigmas)[ncorx == max(ncorx)], max(ncorx), pch = 19)
abline(h = origcor)
legend(
  "bottomright",
  lty = c(1, NA, NA),
  pch = c(NA, 1, 19),
  legend = c("Original", "Pseudo-log", "Pseudo-log with optimal sigma")
)
box()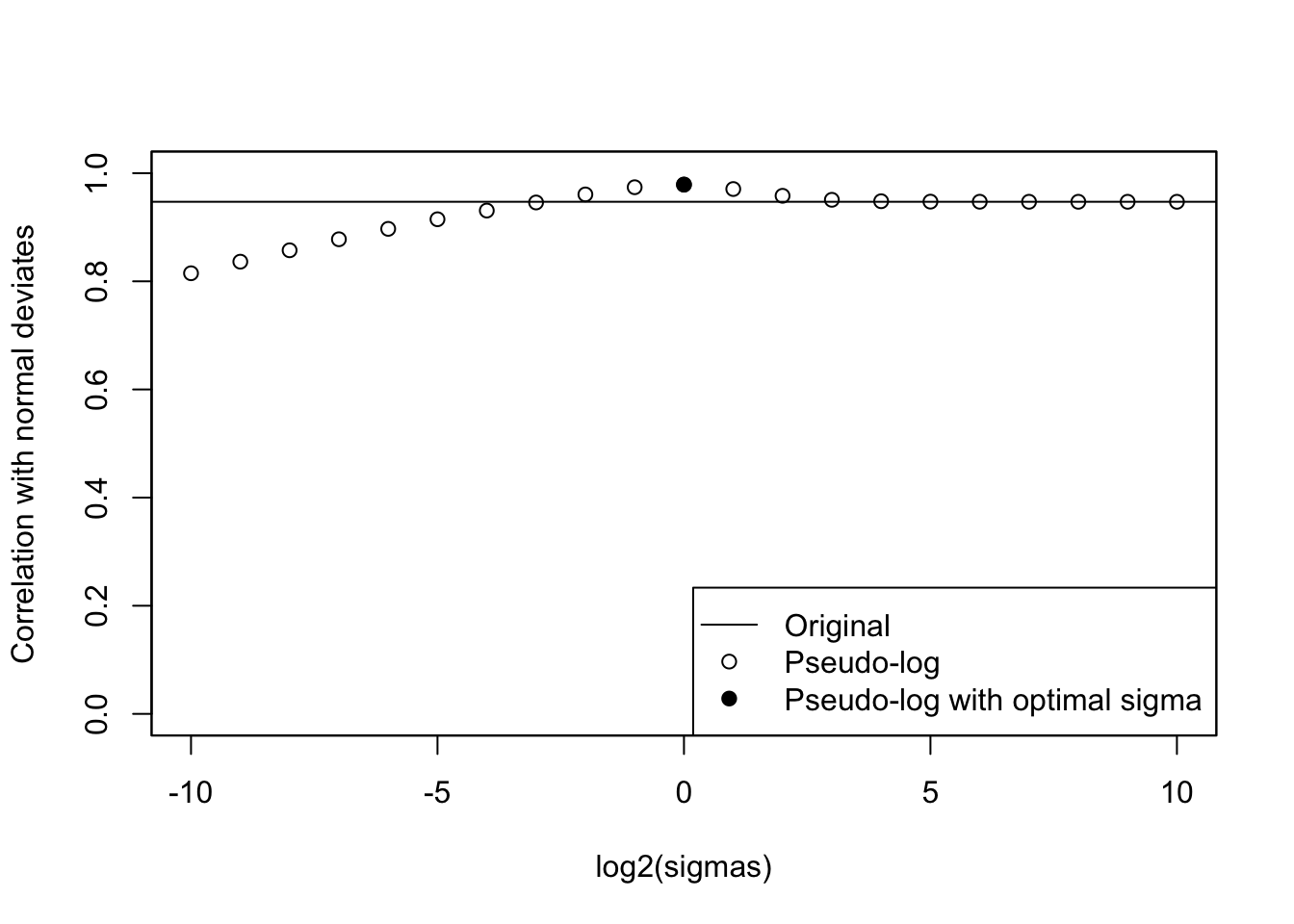

Code 
hist(pseudo_log(x, optsigma))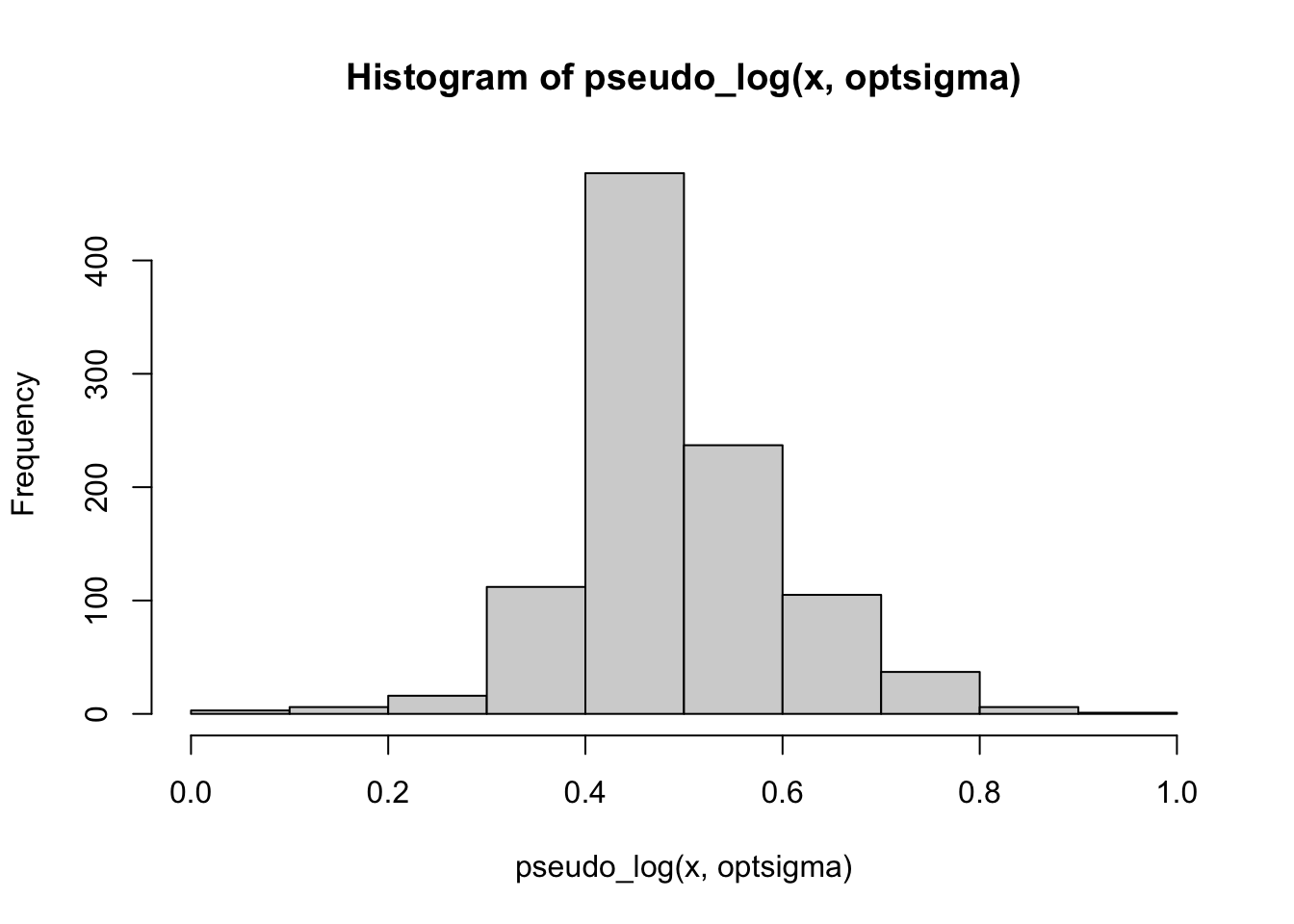

A.3.4 Normal deviates

With simulated normal deviates, the pseudo-logarithm cannot improve the already perfect normality.

Code 
x <- sort(rnorm(1000))

hist(x)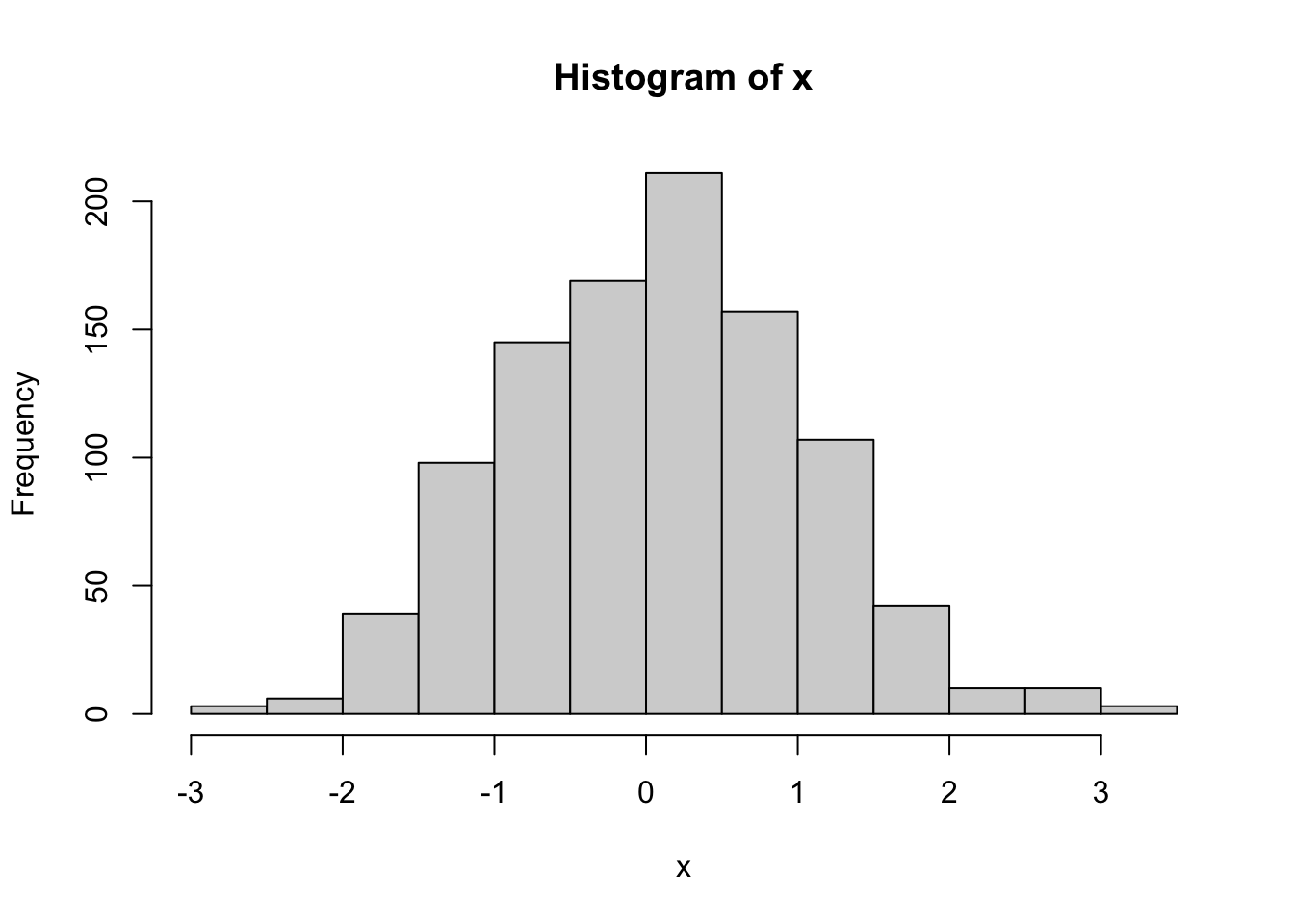

Code 
sigmas <- 2 ** seq(-10, 10, 1)
origcor <- cor(qnorm((1:length(x) - 0.5) / length(x)), x)

ncorx <-
  sapply(sigmas, function(X)
    cor(qnorm((1:length(
      x
    ) - 0.5) / length(x)), pseudo_log(x, X)))

cat("Optimal sigma: ")
Optimal sigma:
Code 
(optsigma <- sigmas[ncorx == max(ncorx)])
[1] 4
Code 
plot(log2(sigmas), ncorx, ylab = "Correlation with normal deviates", ylim =
       c(0, 1))
points(log2(sigmas)[ncorx == max(ncorx)], max(ncorx), pch = 19)
legend(
  "bottomright",
  lty = c(1, NA, NA),
  pch = c(NA, 1, 19),
  legend = c("Original", "Pseudo-log", "Pseudo-log with optimal sigma")
)
abline(h = origcor)
box()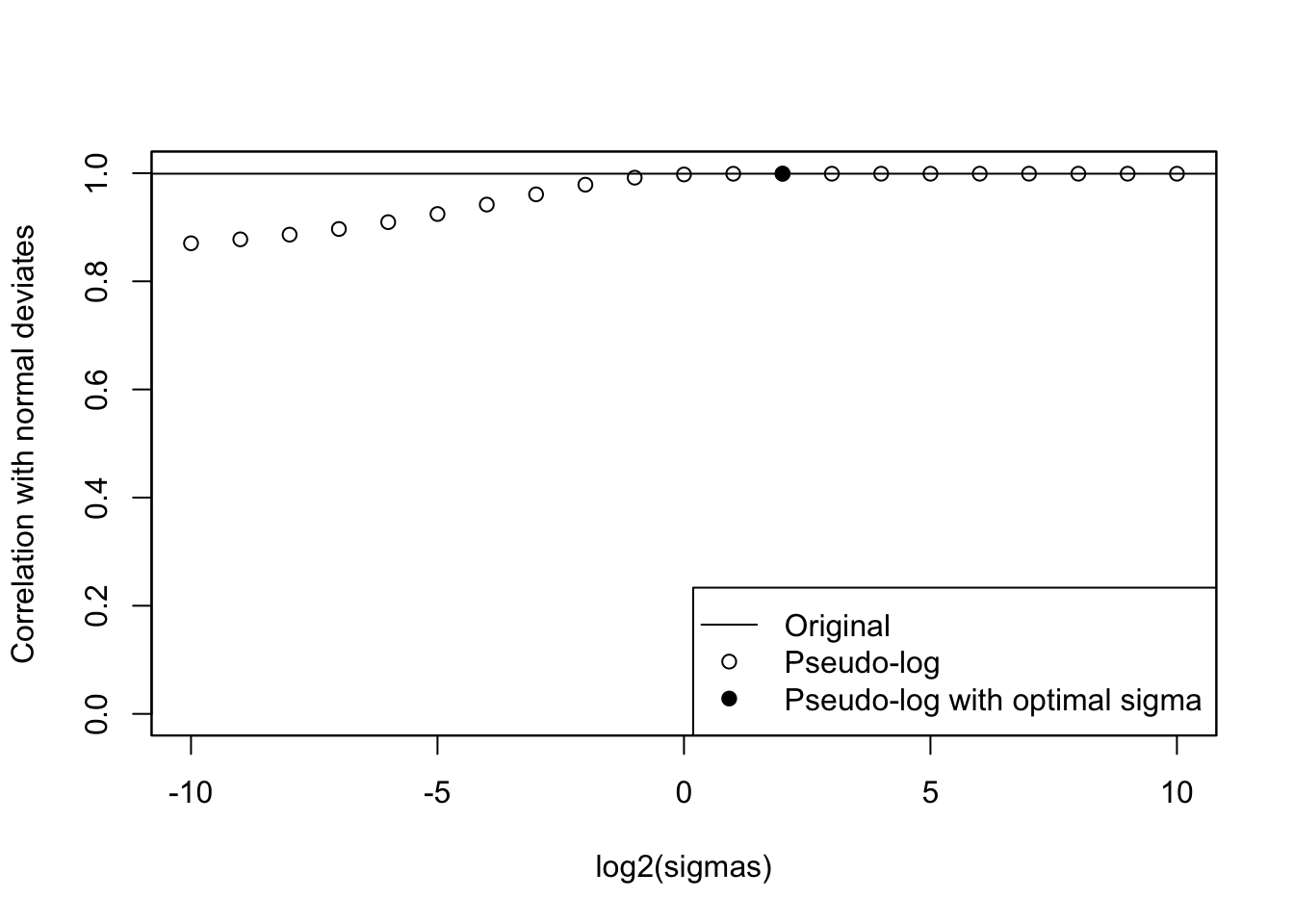

Code 
hist(pseudo_log(x, optsigma))